|
:: 게시판
:: 이전 게시판
|
- 모두가 건전하게 즐길 수 있는 유머글을 올려주세요.
- 유게에서는 정치/종교 관련 등 논란성 글 및 개인 비방은 금지되어 있습니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
14/10/29 21:23
가정
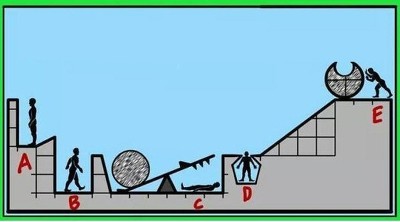
1. 미끄러짐 없음. 2. 두 공의 밀도 , 바깥 지름 동일. 3. 시소는 이상적인 강체 답 D 이유를 더 적어보자면, 공의 반지름은 1이니까 둘레는 2pi = 6 현재 공의 위치와 D의 위치까지 거리는 0.5 + 5 (피타고라스 법칙에 의해) + 0.5 = 6 가정 1에 따라 공이 한바퀴 도니까 D는 머리 찍히고 사망. 굴러온 공이 지렛대 올라갈 때, 지렛대의 높이는 굴러온 공의 높이와 같으므로 포텐션은 없고, 운동에너지만 있는 상태. 왼쪽 공이 더 무겁고 지렛대는 이상적인 강체(가정 2)이니 지렛대는 아래로 내려오지 못하므로 C 생존. 공은 운동에너지에 의해 계속 굴러 턱을 넘어가고, 오른쪽 공과 부딪힌 후 정지.
14/10/29 21:25
대략 눈금들이 있으니 물리적으로 유추 될거 같기는 한데.. D는 머리를 넣을 수 있고, C는 찔리기만 하면 죽는다 하는 전제가 있어야 할 것 같습니다. (아 굴리는 공의 빈 부분에 D의 머리가 세이브 될 수도 있군요!) 아 공도 밀도가 똑같으므로 미는공에서 저 면적을 뺀게 500kg이니 밑에 있는 공은 몇kg이다 라고 계산 가능하겠고요. 저는 이 전제라면 일단 C 사망에 한표입니다.
14/10/29 21:35
가벼운공은 눈금에 따르면 3눈금이고 무거운공은 2눈금만 올라가면 되니깐 W=FS 가 같다면 F=mg이므로 굴린 공의 무게가 높인 공의 무게의 2/3 이상만 되면 내려가는거 아닌가요? 아 20여년만에 물리 생각하니 머리가 터지겠습니다 크크크
14/10/29 21:40
아, 지렛대 중앙으로부터 거리가 다르다고 생각하셨군요.
전 공이 굴러올 쯤이면 왼쪽공도 왼쪽 끝으로 굴러가서 거리는 같은 것으로 봤습니다.
14/10/29 21:43
아뇨 그냥 단순하게 높이에서 떨어진 위치 에너지가 있고 그게 지렛대 턱에서 걸려서 힘의 전환이 아래로 걸려서 비록 무게는 작지만 내려간다고 생각했는데.. 이게 일인가요 운동량 충격량인가요? 아 정말 머리가 돌이 됬네요..
14/10/29 21:50
전 시소 끝의 위치가 굴러온 공의 지면 높이와 일치해서 위치에너지는 없는 것으로 생각했었습니다.
Zel님 처럼 높이차가 있어 위치에너지가 있어서 약간이나마 수직방향 낙하속도가 있다고 하면 운동량 관점에서 봐야하고, 따라서 시소중심을 기준으로 각운동량 보존 법칙을 적용해보면(거리는 좌우 같음, rM(v1)=rm(v2), M>m, v2=굴러온 공 수직방향 낙하속도, v1=기존 공 상승 속도) 무게차이에 의해 오른쪽 공이 떨어지는 높이보다 약간 낮은 정도로 왼쪽 공이 뜬 후 결국 C가 찔리기 전에 왼쪽 공이 다시 떨어져서 C 가 살겠네요. 거기에 굴러온 공은 운동에너지에 의해 의해 왼쪽으로 굴러가버릴테니, 이래나저래나 C가 죽을 일은 없어보입니다.
14/10/29 21:27
D가 안죽으면 아무도 안죽을거 같습니다.
속도가 있어서 바로 지렛대를 눌러 c가 죽진 않고 지렛대 넘어가서 돌 돌 c 모양으로 있을 것 같네요.
14/10/29 21:27
음 C아닌가요? D야 살가능성은 있지만 C는 E가민 공이 위치에너지로인한 운동에너지(?)가 더해져 왼쪽공을 움직일힘이 있어보이는데 그리고 그 힘이 강해서(아주 높은곳에서 떨어뜨리면) 왼쪽공이 뜨고 (이 공 아래 판자가 또 구부려져서 있어) E쪽으로 날아가다 중간이든 어디든지 부딪혀서 다시 내려오면
C는. . . 콘스탄틴에서처럼 E를 향해 거한 손가락욕을 날리고 그분뵈러갈듯 .. .
14/10/29 21:31
D의 위치는 공이 굴러가는 도중에 공의 비어있는 공간 안으로 머리가 들어가느냐 마느냐가 중요한것 같네요.
머리를 안쪽으로 집어넣는다는 가정은 없을것 같습니다.
14/10/29 21:33
일단 눈금하나당 1이라고하면 D는 죽네요.
언덕의 길이는 5에다가 머리가 있는위치까지하면 대략 5.5정도되는데 공의 반지름이 1이니까 반바퀴도는데 대충 3.1, 다음 구멍까지 돌아오려면 9.2니까 일단 D는 사망합니다.
14/10/29 21:37
3정도 돌아도 죽지않나요? 지금 굴리는 위치에서 D의 머리까지 거리가 아무리 잘봐줘도 6이라고쳐도
한바퀴면 딱 6이니까 뚫린부분이아니라 막힌부분이네요. 아, 제가 댓글을 난독했나보네요. 아예 구의 반지름을 0.3정도로 가정한걸 말씀하셨네요.
14/10/29 21:41
표현을 애매하게 썼는데 3만큼이라는게 반바퀴 미끄러진다는 뜻이었습니다.
6만큼 가는 동안 반바퀴 미끄러진다면 6+3 해서 9니까 안죽을 수도 있을 것 같습니다. 근데 전 그냥 안미끄러지는 것으로 생각해서 D 는 확정죽음
14/10/29 21:33
E가 굴리는 공의 뚫린부분에 대한 정보가 더 필요하지 않나요?
뚫린부분은 원인가? 그렇다면 반지름은? 큰원과 작은원의 중심거리는 얼마인가...정도를 알면 누군가 해결해주실거같네요.
14/10/29 21:39
이미지검색하다가 찾게 된 플래시짤입니다. 개그로 만들었다는데 그럴듯하게 보이는건 웰까요.
http://fun.jjang0u.com/chalkadak/view?db=160&no=199796
14/10/29 21:39
일단 d가 안죽더라도 c는 절대 안죽어요 공이 지렛대 끝을 건너 뛰고 중간에 멈추거든요 고로 d가 죽거나 다 살거나 둘중 하나에요
아 저 지레에 놓여진 공의 무게를 생각 안했네요; 그 무게에 따라 달라질듯용 생각하면 할수록 변수가 엄청 많네요 크크 저 공이 미끌어지기 시작하면 굴러가는거에 미끌어지는거까지 포함해야하니..
14/10/29 21:41
세밀하게 따지면 e가 없어서 아무도 안죽음. 장난입니다.
일단 D가 서있는 위치와 공의 사이 거리가 6.xx얼마로 보이는데 공의 지름이 2이므로 원주는 6.28정도 한바퀴 도니까 머리와 부딪힐꺼 같고요. 완전한 공과 구멍난 공의 무게차이는 반지름이 0.5인 구로 가정하면 대략 1/8정도니 40킬로정도 차이 그냥 굴려서 완전한 공 옆에 있을꺼 같긴하네요.
14/10/29 21:49
공이 밀리면 D가 머리를 구덩이로 숨긴다면 살꺼같고 C는 가시에 찔려 죽을거 같네요.
그전에 E가 공을 500Kg공 밀다가 안밀려서 홧병걸려 죽겠죠
14/10/29 21:57
곰곰히 생각해보니까 공이 한바퀴돌아 D는 죽고
왼쪽공이 왼쪽으로 날아갈리는 없고 뜨더라도 제자리에서 뜨겠죠. A,B생존 왼쪽공이더무거우니까 C도 생존. D만 죽나보네요
14/10/29 22:14
위기탈출 넘버원 ver.
E - 돌이 둥글지만 무거워 돌이 밀리지 않자 힘을 쓰다 고혈압으로 사망 D - 무서워서 사망 C - 돌이 떨어질까 겁나서 죽음 B - 상황을 보고 밖으로 나가려다 헛딛어 머리를 부딪혀 사망 A - 뒤를 돌아보고 있어 상황을 몰라 궁금해 죽음
|
||||||||||||