|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
24/11/15 08:22
각도 구하는 문제들은 일부러 그림을 조잡하게 그리는 경향이 있었던 걸로 기억합니다.
각도기로 재 보거나, 눈치로 때려맞히는 걸 막기 위해서 말이죠.. 흐흐흐.
24/11/15 11:25
아닙니다. 그 반대입니다
오히려 각도기 대보면 바로 정답 나오게 그림 출제 합니다 길이 각도 구하는 거면 실측하면 맞게끔 합니다 틀리게 하면 그게 더 문제의 소지가 커서 절대로 조잡하게 내지 않습니다 오히려 눈치로라도 때려맞춰라 그렇게 정답율 올리는게 더 큰 목표입니다.
24/11/15 11:26
뭐... 제 학창시절이야 80년대에서 90년대이니까요. 흐흐흐.
중학생 때 이런 문제 많이 풀었었는데.. 각도기로 재면 무조건 오답 나오도록 출제하셨던 것으로 기억합니다.
24/11/15 12:50
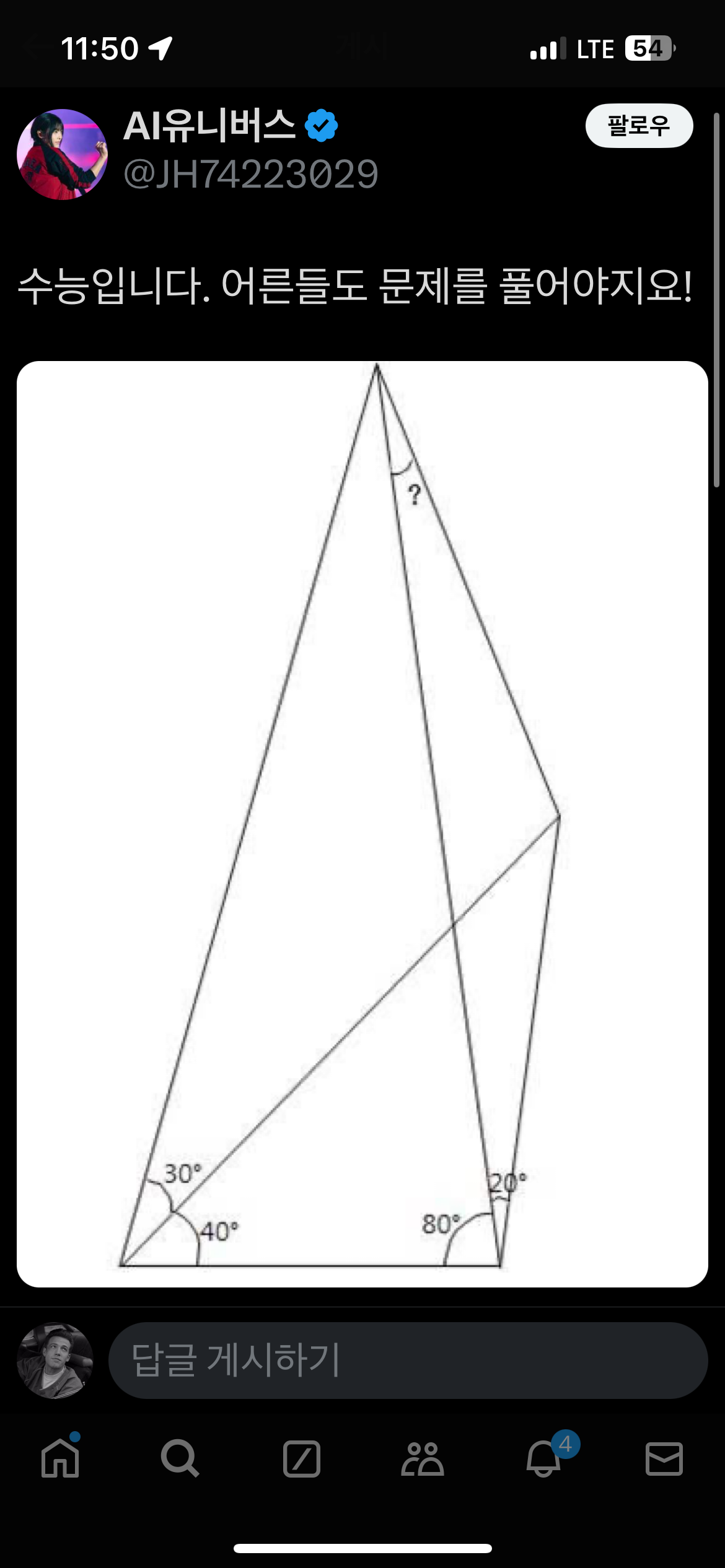
수능은 아니고 일반적인 난이도도 아닙니다. 기하적으로 답은 있고 삼각함수적으로는 풀수는 있을텐데 중학수학의 방식으로 풀이가 있을지는 모르겠네요. 삼각함수 문제풀이는 검색하니 20으로 나오네요.
24/11/15 18:03
(수정됨) ?표가 있는 꼭지점부터 시계 방향으로 돌아가며 순서대로 꼭지점 A, B, C, D라고 합시다.
꼭지점 B에서 선분 AC에 수직이 되게 왼쪽으로 쭉 보조선을 긋습니다. 이 보조선이 선분 AD와 만나는 점을 E라고 합시다. 이 때, 주어진 각도를 통해 계산하면 각 CBD는 40도, 각 EBD는 30도입니다. 따라서 삼각형 BCE와 삼각형 DCE는 합동입니다. 선분 BD와 CE는 직교하고, 그에 따라 각 BCE는 50도, 각 ACE는 30도가 됩니다. 한편 각 EAC도 30도, 각 ACE도 30도이므로, 삼각형 AEC는 이등변삼각형이고 삼각형 AEB와 CEB는 합동입니다. 즉 삼각형 ABC도 이등변삼각형입니다. 따라서 ? = 20도입니다.
|
||||||||||||